Algorithmen zur Schleifbearbeitung von Freiformflächen

(Diplomarbeit Kurzfassung)

	Prüfer:	Prof. Susanne Harms
	2. Prüfer:	Dipl.-Math. (FH) Matthias Güßmann
	Externer Betreuer:	Dipl.-Math. (FH) Matthias Güßmann
	Die Diplomarbeit wurde bei der Firma Itterheim Softwaretechnik -Beratung und Entwicklung- erstellt.

	Problemstellung
	Im Bereich des Werkzeug- und Freiformschleifens können die zu bearbeitenden Geometrien sehr komplex sein.. Um solche Geometrien schleifen zu können werden sie in verschiedene Teilbereiche unterteilt, die nacheinander geschliffen werden.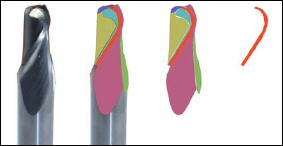
		Die Aufgabe bei dieser Diplomarbeit ist es Flächenbereiche in Verbindung mit einer gegebenen Schleifscheibe zu schleifen. Die betrachteten Positionen müssen dabei flächen- und werkstückskollisionsfrei bearbeitet werden.
	Die Eingangsdaten sind hierbei die Geometrieinformationen der Schleifscheibe und der zu schleifenden Fläche. Die Untersuchungen werden für parametrische sowie diskrete Daten durchgeführt. Für die Implementation wird auf den diskreten Fall zurückgegriffen, da sich parametrische Daten leicht in diskrete Daten konvertieren lassen.

	Durchführung
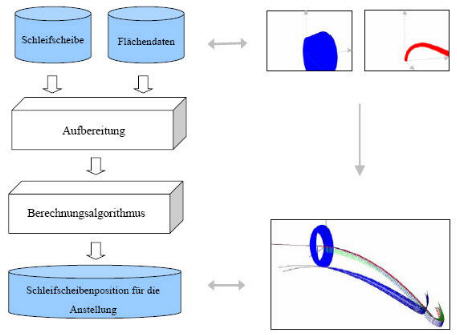
	Bei der Durchführung wird ein Algorithmus verwendet, der wie folgt veranschaulicht werden kann.

	Aus den gegebenen Eingangsdaten (Schleifscheibe und Flächendaten) wird mittels einer Datenaufbereitung ein Datensatz ermittelt, welcher an den eigentlichen Berechnungsalgorithmus übergeben wird. Durch die Aufbereitung der Daten kann eine Ausgangslage geschaffen werden, die gleichbleibende Bedingungen für die Berechnung garantiert. Für die Anstellberechnung werden Transformationen, Schnitt- und Krümmungs-berechnungen sowie die eigentliche Kollisionsbetrachtung verwendet. Die Transformationen werden für die Verbindung von Flächen- und Schleifscheibenbereich verwendet. Dies ist von Interesse, da bestimmte Berechnungen im Schleifscheibenbereich durchgeführt werden und die Ergebnisse in den Flächenbereich übertragen werden müssen und umgekehrt. Die Krümmungs- und Schnittberechnungen werden benutzt, um in der Kollisionsprüfung Methoden herzuleiten, mit denen eine Kollision festgestellt werden kann. Des weiteren werden hieraus Vorgehensweisen erstellt mit denen im Falle einer Kollisionsfeststellung eine Position gefunden wird in der keine Kollision vorliegt. Unterschiede bei den Strategien der Kollisionsvermeidung ist die Ermittlung der Richtung und Länge in der die Schleifscheibe verschoben werden muss. Durch technologische Gegebenheiten können solche Richtungen auch vorgegeben werden, z.B. wenn sich die Schleifscheibe nur um bestimmte Achsen drehen bzw. verschieben kann.

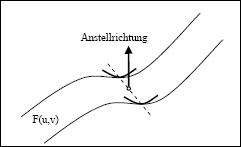
Die nebenstehenden Bilder zeigen eine Situation, in der eine Kollision festgestellt wird (oben) und eine mögliche Ausgleichsposition (unten). Hierbei wird eine Ausgleichsbewegung in Richtung der Flächennormale gewählt. Alternativ könnte hier eine senkrechte Abhebung nach oben gewählt werden.

Zusammenfassung/Ausblick

Durch den in der Diplomarbeit erarbeiteten Algorithmus, lassen sich Flächenbereiche in Verbindung mit einer gegebenen Schleifscheibe schleifen. Um komplexe Geometrien schleifen zu können müssen diese in verschiedene einfache Teilbereiche zerlegt werden, die dann bearbeitet werden. Um einen gleichmäßigen Verlauf der Schleifscheibe gewährleisten zu können müssen Ecken mit einen minimalen Radius verrundet werden. Durch die Verrundung kann es vorkommen, dass Material stehen bleibt, welches eigentlich mit abgetragen werden sollte, dies ist besonders in Innenecken der Fall. Eine Vorgehensweise die zukünftig hier einsetzen könnte würde eine andere Schleifscheibe vorschlagen, mit welcher die Fläche genauer geschliffen wird. 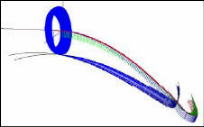Die folgenden Bilder zeigen nun noch ein paar Flächen, die mit dem Algorithmus bearbeitet werden.

Konturzug - Modellierung

(Praktikum ISBE)

	Aufgabenstellung war die Modellierung und Implementierung eines Modules, mit dem man eine Kontur aus Kreis- und Geradenstücken modellieren kann. Für die Realisierung wurde mit Visual C++ und Windows-Grafikfunktionen verwendet, ausserdem kamen die Microsoft Foundation Classes (MFC) und die Active Template Library (ATL) zum Einsatz.
	Anwendungsbeispiel
	Ausgangssituation: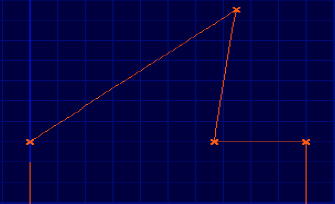	Es wurde eine Kontur aus mehreren Strecken modelliert, so dass eine Spitze entstanden ist, welche nun abgerundet werden soll. Hierzu werden die zwei Strecken ausgesucht, die verrundet werden sollen.
	Durchführung: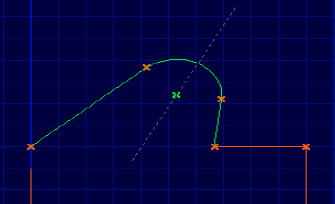	Nachdem die beiden Strecken der Spitze ausgewählt wurden, sieht man den abgerundeten Kreisbogen. Jetzt kann man am grün gekennzeichneten Mittelpunkt den Radius des Kreises (via Mausbewegung) verändern. Hierbei findet immer eine Projektion der Mauskoordinaten auf die getrichelte Winkelhalbierende statt, um definierte Randbedingungen nicht zu variieren.
	Extremas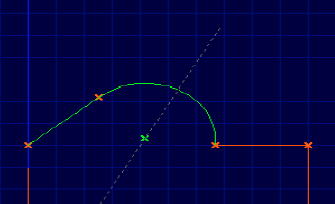	In diesem Bild sieht man nun eines der Extremas, die für den eingefügtem Kreis möglich sind. Der Kreis kann hier nich weiter vergrößert werden, da die Grenzen der Ausgangsstrecke (rechts, Befrenzung durch waagrechte, rote Strecke) erreicht sind.

Gabelstapler-Animation

(Studienarbeit)

Die Studienarbeit wurde während des 3. Semesters in Begleitung zur Vorlesung "Grafische Datenverarbeitung" angefertigt.

Gefordert war die Animation von Objekten, außerdem sollte man interaktiv auf das Geschehen Einfluss nehmen können.

Für meine Arbeit habe ich dabei einen Gabelstapler in einer (vereinfachten) Lagerhalle gewählt.

Die Anwendung hat zwei verschiedene Modi, der eine ist eine Simulation, der andere eine eigene Steuerung.

Im Simulationsmodus wird per Zufallsgenerator eine Kiste gewählt und dann an eine andere zufällige, freie Position verschoben.

Im Entscheidungsmodus kann in einem separatem Steuerungsfenster die Kiste gewählt werden, die verschoben werden soll und die Zielposition festgelegt werden.

Weitere Interaktionsmöglichkeiten:

Änderung der Darstellung (Perspektive):
Es kann zwischen einer perspektiven Darstellung (siehe oben) und zwei orthogonalen Darstellungen gewechselt werden. Die Orthogonalen Darstellungen sind eine Senkrechte Projektion von oben bzw. von der Seite.

Änderung der Lichteinstellung:
Verschiedene Lichter können an und ausgeschaltet werden.

Änderung der Kistenanzeige:
Auf den Frontseiten der Kisten können Textur-Bilder angezeigt werden, es stehen dabei 3 Bilder zur Verfügung, eines ist von meinem Professor, eines von einem Assistenten, der bei der Vorlesung geholfen hat und eines von mir.

Änderung der Kistenanzahl:
In einem gewissen Bereich kann die Anzahl der Kisten bestimmt werden, die Mindestanzahl sind 2 Kisten, Maximal sind es 19 Kisten, damit noch die Möglichkeit besteht, Kisten zu verschieben.

Zusätzliche Ansicht:
Bei Bedarf kann man ein weiteres Fenster öffnen, in dem die Sicht aus dem Gabelstapler dargestellt wird.